위상정렬에서 사이클 여부를 검증하는 칸 알고리즘

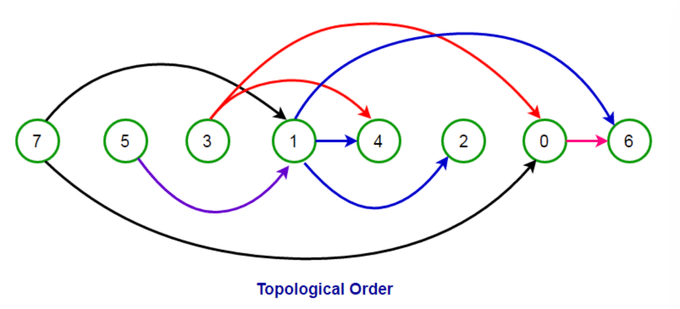
위상 정렬

위상 정렬은 그래프 이론에서 중요한 알고리즘 중 하나로, 방향 그래프의 모든 노드를 순서대로 나열하는 방법입니다. 특히, 사이클이 없는 방향 그래프(DAG, Directed Acyclic Graph)에서 그래프의 각 노드 간의 순서를 결정하는 데 사용됩니다. 위상 정렬은 작업의 우선순위 설정이나 프로젝트의 작업 계획, 강의 순서 정하기 등 다양한 곳에서 활용됩니다.

칸 알고리즘(Kahn's Algorithm)

위상 정렬을 구현하는 알고리즘 중 하나로 “칸 알고리즘(Kahn's Algorithm)”이 있습니다. 칸 알고리즘은 위상 정렬을 구하는 데 있어 직관적이며 효율적인 방법을 제공합니다. 이 알고리즘은 진입 차수(in-degree)에 기반한 접근을 사용하여, 각 노드가 다른 노드로부터 들어오는 간선의 수를 추적합니다. 진입 차수가 0인 노드를 찾아 순서대로 처리하면서 그래프를 위상 정렬하는 방식입니다. 이를 통해 사이클이 없는 방향 그래프의 모든 노드를 올바른 순서로 나열할 수 있습니다.

칸 알고리즘의 작동 원리

칸 알고리즘의 주요 아이디어는 '진입 차수가 0인 노드를 큐에 넣고, 이를 하나씩 처리하며 해당 노드에서 나가는 간선을 제거하는 것'입니다. 이 과정을 반복하면 모든 노드를 위상 정렬된 순서로 나열할 수 있으며, 이를 통해 그래프가 사이클을 가지는지 여부도 판단할 수 있습니다. 만약 모든 노드를 처리하지 못했다면 그래프에는 사이클이 존재한다는 의미입니다.

파이썬 코드 예제

아래는 칸 알고리즘을 파이썬으로 구현한 예시 코드입니다.

from collections import deque

def kahn_topological_sort(graph):
    # 각 노드의 진입 차수를 저장합니다.
    in_degree = {node: 0 for node in graph}
    for node in graph:
        for neighbor in graph[node]:
            in_degree[neighbor] += 1

    # 진입 차수가 0인 노드를 큐에 추가합니다.
    queue = deque([node for node in in_degree if in_degree[node] == 0])
    topological_order = []

    while queue:
        current_node = queue.popleft()
        topological_order.append(current_node)

        # 현재 노드에서 나가는 간선을 제거하고, 해당 간선의 목적지 노드의 진입 차수를 감소시킵니다.
        for neighbor in graph[current_node]:
            in_degree[neighbor] -= 1
            if in_degree[neighbor] == 0:
                queue.append(neighbor)

    # 모든 노드를 처리했는지 확인합니다.
    if len(topological_order) == len(graph):
        return topological_order
    else:
        raise ValueError("그래프에 사이클이 존재합니다.")

# 그래프 예시
graph = {
    'A': ['C'],
    'B': ['C', 'D'],
    'C': ['E'],
    'D': ['F'],
    'E': ['H', 'F'],
    'F': ['G'],
    'G': [],
    'H': []
}

try:
    result = kahn_topological_sort(graph)
    print("위상 정렬 결과:", result)
except ValueError as e:
    print(e)

이 코드는 방향 그래프를 입력으로 받아 위상 정렬된 순서를 출력합니다. in_degree 딕셔너리를 통해 각 노드의 진입 차수를 기록하고, 진입 차수가 0인 노드들을 queue에 추가하여 차례로 처리합니다. 만약 모든 노드를 처리하지 못하고 큐가 비게 된다면, 이는 그래프에 사이클이 있음을 의미합니다.

시간 복잡도

칸 알고리즘은 큐를 사용하여 그래프를 순서대로 처리하므로, 시간 복잡도는 O(V + E)입니다. 여기서 V는 노드의 개수, E는 간선의 개수를 나타냅니다. 이 점에서 칸 알고리즘은 위상 정렬을 수행하는 효율적인 방법으로 손꼽힙니다.