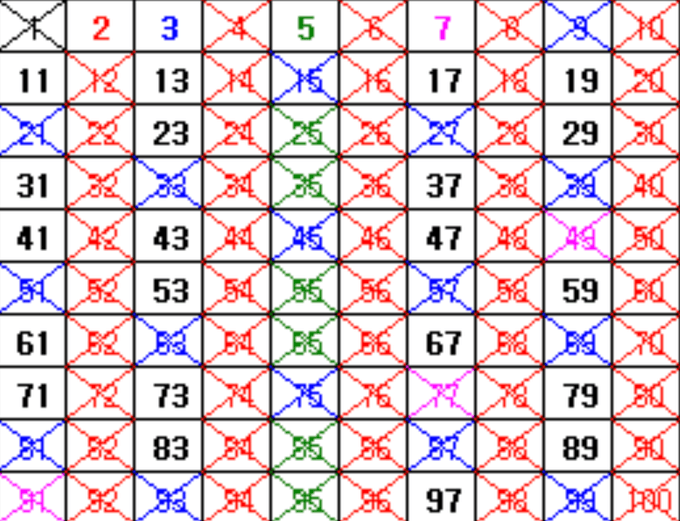
에라토스테네스의 체
에라토스테네스의 체(Sieve of Eratosthenes)는 소수를 찾기 위한 고대 그리스 수학자 에라토스테네스가 고안한 알고리즘입니다. 이 알고리즘은 일정 범위 내의 모든 소수를 효율적으로 구하는 방법으로, 단순한 반복적인 방식보다 훨씬 빠르게 소수를 걸러낼 수 있습니다.
사용 이유
에라토스테네스의 체는 빠르고 효율적으로 소수를 구할 수 있다는 점에서 매우 유용합니다. 시간 복잡도가 으로, 단순한 반복과 나눗셈을 통해 소수를 판별하는 방법보다 훨씬 빠릅니다. 특히 소수 판별이 필요한 큰 범위에서 사용하기 적합합니다. 이 알고리즘은 수학적 문제나 코딩 테스트에서 자주 사용되며, 소수와 관련된 문제를 빠르게 해결하기 위해 필수적인 도구입니다.
동작 원리
- 먼저 2부터 시작하여 특정 수의 배수들을 지워 나갑니다.
- 소수를 하나 찾을 때마다 해당 소수의 배수를 모두 지워나갑니다. 이를 반복하면 소수만 남게 됩니다.
- 최종적으로 지워지지 않은 수들이 모두 소수가 됩니다.
파이썬 구현
다음은 파이썬으로 에라토스테네스의 체를 구현한 코드입니다:
def sieve_of_eratosthenes(limit):
# 모든 수를 소수로 가정하고 리스트 초기화
is_prime = [True] * (limit + 1)
is_prime[0] = is_prime[1] = False # 0과 1은 소수가 아님
for number in range(2, int(limit**0.5) + 1):
if is_prime[number]:
# 현재 수의 배수를 모두 소수가 아닌 것으로 마크
for multiple in range(number * number, limit + 1, number):
is_prime[multiple] = False
# 소수인 수들만 리스트로 반환
primes = [num for num, prime in enumerate(is_prime) if prime]
return primes
# 예시 사용
limit = 50
print(sieve_of_eratosthenes(limit))위의 코드에서 limit 변수는 소수를 구하고자 하는 범위의 최대값을 의미합니다. 예를 들어, limit = 50으로 설정하면 2부터 50 사이의 모든 소수를 구하게 됩니다. 코드의 주요 단계는 다음과 같습니다:
- is_prime 리스트 초기화:
True로 초기화된 리스트로, 각 인덱스가 해당 숫자가 소수인지 여부를 나타냅니다. - 반복문으로 배수 제거: 각 소수의 배수를
False로 설정하여 소수가 아닌 것으로 표시합니다. - 소수 리스트 반환: 최종적으로
True로 남아 있는 인덱스가 소수입니다.
시간 복잡도
에라토스테네스의 체의 시간 복잡도는 (O(n \log \log n))입니다. 이는 단순하게 모든 수에 대해 나눗셈을 수행하는 방법보다 훨씬 효율적입니다. 알고리즘은 기본적으로 각 수의 배수를 지우기 때문에 복잡도가 크게 증가하지 않으며, 많은 수의 소수를 빠르게 찾는 데 적합합니다.
활용 사례
- 소수 관련 문제 해결: 코딩 테스트나 알고리즘 문제에서 일정 범위 내의 소수를 구해야 할 때 유용합니다.
- 암호학: RSA와 같은 암호 알고리즘에서는 큰 소수를 찾는 것이 중요한 역할을 합니다.
결론
에라토스테네스의 체는 매우 효율적인 소수 찾기 알고리즘으로, 간단하면서도 강력한 방법입니다. 특히 큰 범위의 소수를 빠르게 찾아야 하는 경우에 강력한 도구가 될 수 있으며, 수학적 문제뿐만 아니라 실생활의 다양한 분야에서도 응용됩니다.